МОДЕЛЬ ЗАМЕДЛЕНИЯ СТАРЕНИЯ ЧЕЛОВЕКА

Опубликовано в книге: Процессы управления и устойчивость: Труды XXXIII научно-практической конференции студентов и аспирантов факультета ПМ-ПУ СПбГУ 15-18 апреля 2002г. - СПб: ООП НИИ Химии СПбГУ, 2002. - с. 287-292.

МОДЕЛЬ ЗАМЕДЛЕНИЯ СТАРЕНИЯ ЧЕЛОВЕКА

Минвалеев Р.С., Иванов А.И.
Санкт-Петербургский государственный университет

Изложены результаты, найденные в ходе исследований специфических постуральных влияний на различные характеристики внутренней среды организма человека [1]. Результаты предыдущих исследований опубликованы в работах [2-4], а также защищены в диссертации [5]. Найденный в диссертации [5] подход к изучению физиологических механизмов постуральных влияний на системный и внутриорганный кровоток позволил обозначить комплексную проблему поиска моделей возможных быстрых гормональных реакций в ответ на специфические постуральные воздействия у здоровых людей.
В работе [6] найдена стохастическая модель изменения концентрации кортизола в сыворотке крови человека в ответ на возмущающее воздействие бхуджангасаны - одной из ключевых практик хатха-йоги. Техника выполнения бхуджангасаны изложена в книге [7]. Настоящая работа имеет целью изложение результатов статистической проверки гипотезы изменения численных значений характеристик концентрации основных стероидных гормонов сыворотки крови в ответ на применение бхуджангасаны как системы управления. В таблице 1 напечатаны результаты измерений концентрации гормонов в сыворотке крови до и после бхуджангасаны. По утверждению проводившей измерения организации (Клинико-диагностическая лаборатория Медицинской академии последипломного образования (Санкт-Петербург)), коэффициент вариации k=0.08 найден с учетом того, что количественное определение каждого из результатов измерений выполнялось 10 раз.

ТАБЛИЦА 1. КОНЦЕНТРАЦИЯ КОРТИЗОЛА И ТЕСТОСТЕРОНА В КРОВИ 

Применением K-S-критерия доказано, что гипотезы о принадлежности к нормально распределенным генеральным совокупностям 4-х выборок, напечатанных в столбцах 2-5 таблицы 1, отклоняются.
Выполним постановку задачи.
1. По выборочным данным из таблицы 1 найти аналитические выражения функции распределения непрерывных случайных величин, из генеральных совокупностей численных значений которых извлечены выборки, напечатанные в столбцах 2-5 таблицы 1.
2. Найти доверительные интервалы математических ожиданий этих случайных величин с надежностью γ≥0.95, накрывающие численные значения математических ожиданий. Применим новый метод, найденный А.И.Ивановым и опубликованный в приложении к книге [9] В.И.Зубова, в работах [10, 11]. Программная реализация метода изложена в работе [12].
Запишем аналитические выражения функции распределения случайных величин, выборки численных значений которых напечатаны в столбцах 2-5 таблицы 1. В общем виде аналитическое выражение указанных функций распределения записывается как

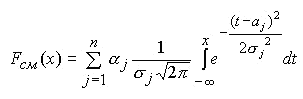
где F_см(x) - функция распределения смесь нормальных распределений. Аналитические выражения функции распределения случайных величин, выборки численных значений которых напечатаны в столбцах 2 и 3 таблицы 1, опубликованы в работе [6]. Уровни значимости, с которыми приняты гипотезы о моделях законов распределения равны α=0.001. Применением нового метода (А.И.Иванова) математической обработки результатов измерений были вычислены границы доверительных интервалов математических ожиданий исследуемых численных значений кортизола с учетом указанного коэффициента вариации k=0.08. Обозначим через Х_с – численное значение математического ожидания концентрации кортизола до опыта, а Y_с – численное значение математического ожидания концентрации кортизола после опыта. Тогда численное значение концентрации кортизола в сыворотке крови до выполнения упражнения бхуджангасаны будет равно Х_с=394.5 и с надежностью γ=0.99 накрыто интервалом (362.1 < Х_с < 426.9). Выполнением такого же расчета доверительного интервала для численных значений концентрации кортизола в сыворотке крови сразу после выполнения упражнения бхуджангасаны находим, что численное значение характеристики равно Y_с=332.6 и с надежностью γ=0.99 накрыто интервалом (305.3 < Y_с < 360). Найденные доверительные интервалы не пересекаются. Сформулируем вывод: с надежностью γ=0.99 можно утверждать, что в результате выполнения испытуемыми упражнения бхуджангасана концентрация кортизола в крови испытуемых уменьшилась. В таблицах 2 и 3 напечатаны численные значения характеристик α_j , a_j , σ_j функций распределения, найденных по выборочным данным из столбцов 4 и 5 таблицы 1 соответственно (для тестостерона).

Уровни значимости, с которыми приняты гипотезы о моделях законов распределения, соответственно равны α=0.03 и α=0.002. Применением нового метода математической обработки результатов измерений, опубликованного в работах [9-11], вычислены границы доверительных интервалов математических ожиданий исследуемых численных значений тестостерона с учетом указанного коэффициента вариации k=0.08. Обозначим через Х_t – численное значение математического ожидания концентрации тестостерона до опыта, а Y_t – численное значение математического ожидания концентрации тестостерона после опыта. Тогда численное значение концентрации тестостерона в сыворотке крови до выполнения упражнения бхуджангасаны будет равно Х_t=15.97 и с надежностью γ=0.95 накрыто интервалом (15.0 < Х_t < 16.88). Выполнением такого же расчета доверительного интервала для численных значений концентрации тестостерона в сыворотке крови сразу после выполнения упражнения бхуджангасаны находим, что численное значение характеристики равно Y_t=18.0 и с надежностью γ=0.95 накрыто интервалом (16.98 < Y_t < 19.04). Найденные доверительные интервалы не пересекаются.
Сформулируем вывод: с надежностью γ=0.95 можно утверждать, что в результате выполнения испытуемыми упражнения бхуджангасана концентрация тестостерона в крови испытуемых увеличилась.

Сформулируем физиологический результат работы. Известно, что с точки зрения нейроэндокринной теории старения [13] возрастные изменения в организме человека, сопровождаются увеличением продукции кортизола (хронический стресс или гиперадаптоз по В.М.Дильману) и снижением функции половых желез (климактерические изменения). В наших опытах специфическое напряжение мышц, сопровождающееся принятием специфической позы тела - бхуджангасаны - статистически значимо (с надежностью γ=0.99 ) снизило на 16% уровень кортизола сыворотки крови у здоровых людей, и с надежностью γ=0.95 повысило на 11% уровень основного мужского полового гормона тестостерона. Найденный и опубликованный в работах [9-11] новый метод нахождения аналитического выражения функции распределения по выборочным данным и нахождения границ доверительных интервалов позволил доказать статистическую значимость изменений концентрации кортизола и тестостерона под влиянием воздействия бхуджангасаны. Найденный результат позволяет сделать статистически обоснованное заключение о том, что практика бхуджангасаны ведет к изменениям, противоположным старению организма человека.

Литература

1. Ebert D. Physiologische Aspekte des Yoga. - Leipzig: VEB Georg Tieme, 1986 - 150 S. (Имеется перевод: Эберт Д. Физиологические аспекты йоги /пер. с нем. Минвалеева Р.С. - СПб., 1999 - 159 с.) 
2. Минвалеев Р.С., Кузнецов А.А., Ноздрачев А.Д., Лавинский Х.Ю. Особенности наполнения левого желудочка сердца при пе-ревернутых позах человека // Физиология человека, 1996, т.22, №6, с.27-34.
3. Минвалеев Р.С., Кузнецов А.А., Ноздрачев А.Д. Как влияет по-за тела на кровоток в паренхиматозных органах? Сообщение I. Печень // Физиология человека, 1998, т.24, №4, с.101-107.
4. Минвалеев Р.С., Кузнецов А.А., Ноздрачев А.Д. Как влияет по-за тела на кровоток в паренхиматозных органах? Сообщение II. Почки // Физиология человека, 1999, т.25, №2, с. 92-98.
5. Минвалеев Р.С. Особенности внутрисердечного и внутриорганного кровотока при избранных позах человека (по данным допплерэхографии). Дисс… канд. биол. наук. - СПб., 1999.
6. Минвалеев Р.С. Бхуджангасана понижает уровень кортизола у здоровых людей // Материалы научно-практической конференции, посвященной памяти В.И.Зубова. СПб., 12-13 января 2002 г. – СПб: 2002 - с.32-42.
7. Смирнов Б.Л. Санкхья и йога // Бхагавадгита. Сер. "Философские тексты Махабхараты" 3-е изд., доп./Введение, пер. с санскр. и коммент. Б.Л.Смирнова. - СПб.: "А-cad", 1994. – с.395-396.
8. Князев Ю.А., Беспалова В.А. Гормонально-метаболические диагностические параметры. Справочник. Приложение к журналу «Врач». - М.: Изд. дом "Русский врач", 2000. - 96 с.
9. Зубов В.И. Проблема устойчивости процессов управления. 2-е изд., испр. и доп.- СПб.: НИИ Химии СПбГУ, 2001. - 354 с.
10. Иванов А.И. Новый метод математической обработки результатов измерений // Материалы научно-практической конференции, посвященной памяти В.И.Зубова. СПб., 12-13 января 2002 г. – СПб: 2002 - с.5-26.
11. Иванов А.И. Доверительный интервал математического ожидания случайной величины с функцией распределения смесь нормальных распределений // Материалы научно-практической конференции, посвященной памяти В.И.Зубова. СПб., 12-13 января 2002 г. – СПб: 2002 - с.27-31.
12. Наборщиков В.Г. Программная система исследования выборочных данных // Материалы научно-практической конференции, посвященной памяти В.И.Зубова. СПб., 12-13 января 2002 г. – СПб: 2002 - с.50-56.
13. Дильман В.М. Большие биологические часы. Введение в интегральную медицину. - М.: "Знание", 1986. - 255 с.